一、问题求解：第1~15小题，每小题3分，共45分。下列每题给出的A、B、C、D、E五个选项中，只有一项是符合试题要求的。

　　1、某部门在一次联欢活动中共设26个奖，奖品均价为280元，其中一等奖单价为400元，其他奖品均价为270元，一等奖的个数为（E）

　　A  6   B  5   C  4    D  3 E2

　　解析：设一等奖有X个，则其他奖项有26-X个。26个奖品的均价为280元，得知总价为26*280元。由题意立方程400X+270（26-X）=26*280。计算得出X=2，所以答案为E

　　2. 某公司进行办公室装修，若甲乙两个装修公司合做，需10周完成，工时费为100万元，甲公司单独做6周后由乙公司接着做18周完成，工时费为96万元，甲公司每周的工时费为（B）

　　A 7.5万元B.7万元   C. 6.5万元D.6万元 E.5.5万元

　　解析：设甲公司每周工时费为X万元，乙公司每周工时费为Y万元。由题意甲乙两个装修公司合做，需10周完成，工时费为100万元得知10（X+Y）=100，

　　即Y=10-X ……①

　　又甲公司单独做6周后由乙公司接着做18周完成，工时费为96万元，

　　得方程6X+18Y=96 ……②

　　将方程①带入方程②，X=7，所以答案为B

　　3. 如图1，已知AE=3AB,BF=2BC,若三角形ABC的面积为2，则三角形AEF的面积为（B）

 

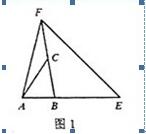
　　A.14  B. 12   C. 10  D.8 E.6

　　解析：做辅助线AD⊥BF，垂足为D，AD即△ABC和△ABF的高。

　　∵S△ABC=2=?BC*AD

　　由题知2BC=FB

　　∴S△ABF=?FB*AD=BC*AD=4

　　做辅助线FG⊥AE，垂足为G，FG即△AFE和△AFB的高。

　　∵3AB=AE, S△ABF=?AB*FG=4

　　S△AFE=?AE*FG=?*3AB*FG=12

　　所以答案为B

　　4. 某公司投资一个项目，已知上半年完成预算的三分之一，下半年完成了剩余部分的三分之二，此时还有8千万投资未完成，则该项目的预算为（B）

　　A.3亿元   B.3.6亿元   C.3.9亿元  D.4.5亿元E.5.1亿元

　　解析：设该项目预算为X亿元。8千万=0.8亿

　　上半年完成（1/3）X元。

　　下半年完成剩余部分（即2/3）的三分之二，即（2/3）*（2/3）X元。

　　由题意立方程：X-(1/3)X-(2/3)(2/3)X=0.8

　　解方程X=3.6

　　所以答案为B

　　5.如图2，圆A与圆B的半径为1，则阴影部分的面积为（E）
       

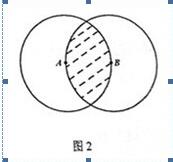
　　解析：做辅助线，两圆相交C、D两点（C在上面，D在下面）。链接AB、CD、AC、AD。AB和CD交于点F。

　　由扇形公式得知：S=（n/360）πr?  ,n是扇形圆心角，r是圆半径。

　　两个圆的半径为1，即AB=AC=CB=1，△ABC为等边三角形。同理，△ABD为等边三角形。∴∠CAB=60°，∠CAD=120°。S扇形=（1/3）πr?=（1/3）π

　　由勾股定理得CD=√3，S△ACD=（?）CD*AF=（√3）/4

　　∴阴影部分面积=2S扇-S四边形ABCD=2S扇-2 S△ACD=（2/3）π-（√3）/2

　　所以答案选E

　　6.某容器中装满了浓度为90%的酒精，倒出1升后用水装满，摇匀后又倒出1升，再用水将容器注满，已知此时酒精浓度为40%，则该容器的容积是（B）

　　A.2.5升   B.  3升  C.  3.5升 D.  4升E.  4.5升.

　　解析：设容器容积为X。得【(X-1)/X】?*0.9=0.4，所以X=3。答案选B

　　7.已知{an}为等差数列，且a2-a5+a8=9，则a1+a2+……+a9=

　　A.27  B.45  C.54  D. 81 E. 162

　　解析：由等差数列性质可知a5-a2=a8-a5，带入a2-a5+a8=9，得a5-a8+a8=9，所以a5=9

　　由等差数列求和公式可知：a1+a2+……+a9=【9（a1+a9）】/2

　　又a1+a9=2a5，所以a1+a2+……+a9=81

　　所以答案选D

　　8.甲乙两人上午8：00分别从A,B两地出发相向而行，9：00第一次相遇，最后速度均提高了1.5公里/小时，甲到B，乙到A后立刻返回，若两人在10：30再次相遇，则A,B两地的距离为（D）

　　A.5.6公里   B.  7公里  C.  8公里 D.  9公里E.9.5公里

　　解析：设AB两地距离为x公里。甲速度为V1，乙速度为V2

　　甲乙两人上午8：00分别从A,B两地出发相向而行，9：00第一次相遇

　　则有公式：X/（V1+V2）=1，即X=V1+V2  ……①

　　速度均提高了1.5公里/小时，甲到B，乙到A后立刻返回，若两人在10：30再次相遇

　　则有公式：2X/（V1+V2+3）=1.5  ……②

　　将①带入②，的2X/(X+3)=1.5，∴X=9

　　所以答案为D
　9. 掷一枚均匀的硬币若干次，当正面次数向上大于反面次数向上时停止，则在4次之内停止的概率是（C）

 

 

　　解析：分类讨论题目。投掷出正面的概率为(1/2)，投掷出反面的概率为(1/2)。

　　若投掷第一次正面向上停止，概率为(1/2)，

　　投掷两次，一次反面一次正面，概率相等，不考虑。

　　若投掷三次，则第一次定为反面，后两次为正面，概率=(1/2)* (1/2)* (1/2)=1/8

　　每种情况的概率相加1/2+1/8=5/8

　　所以答案选C

　　10.若几个质数的乘机为770，则这几个质数的和为（E）

　　A.85 B.  84 C.128  D.26   E.  25

　　解析：770=7*110=7*11*10=7*11*5*2

　　所以7,11,5,2为770的质数之乘。质数和=7+11+5+2=25，所以答案选E

　　11. 已知直线l是圆X?+Y?=5在点（1，2）处的切线，则l在y轴上的截距是（D）

 
　　解析：已知切点坐标，求切线方程

　　过点（X0，Y0）的切线为x*x0+y*y0=r?

　　所以L方程为X+2Y=5，

　　由点斜式方程可知Y=kX+b，b为l在y轴上的截距。

　　转化方程得Y=(-1/2)X+(5/2)

　　所以答案选D

　　12. 如图3，正方体的棱长为2，F是棱的中点，则AF的长为（A）

 

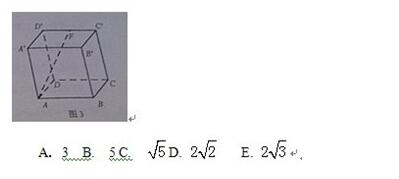
　　解析：做辅助线FG⊥CD，垂足为G，链接AG

　　由题意可知，FG∥CC,DG=?DC=1，AD=2，有勾股定理得AG=√5，AF=√（FG?+AG?）=3

　　所以答案选A

　　13. 在某项活动中将3男3女6名志愿者随机分成甲乙丙三组，每组2人，则每组志愿者都是异性的概率为（E）

　　解析：6个人分甲乙丙三组，每组2人，总共的分法有：C(2，6)C(2，4)C(2，2)=90种。

　　每组志愿者都是异性的分法有：

　　C（1,3）C（1,3）C（1,2）C（1,2）C（1,1）C（1,1）=36种。

　　概率=36/90=2/5  所以答案选E

　　14. 某工厂在半径为5cm的球形工艺品上镀上一层装饰金属，厚度为0.01cm，已知装饰金属的原材料为棱长20cm的正方体，则加工10000个该工艺品需要多少个这样的正方体（C）

　　A.2  B.  3  C.  4   D.  5  E.  20

　　解析：球的体积=球面积*厚度=4πr?*0.01=π，加工10000个所需体积≈31400

　　金属正方体体积=20*20*20=8000

　　31400÷8000≈4
　　所以答案选C

　　15. 某单位决定对4个部门的经理进行轮岗，要求每位经理必须轮换到4个部门的其他部门任职，则不同的轮岗方案有（D）

　　A.3种B.  6种C.  8种D. 9种   E.  10种

　　解析：不看要求总共有4*3*2*1=24种方案

　　四个人都分到自己部门的方案有1种

　　三个人分到自己部门的方案有C(3，4)=4种

　　两个人分到自己部门的方案有C（2,4）=6种

　　一个人分到自己部门的方案有C（1,4）=4种

　　每位经理必须轮换到4个部门的其他部门任职，则不同的轮岗方案有24-1-4-6-4=9种

　　所以答案选D

　　二、条件充分性判断：第16~25小题，每小题3分，共30分。要求判断每题给出的条件（1）和条件（2）能否充分支持题干所陈述的结论。A、B、C、D、E五个选项为判断结果，请选择一项符合试题要求的判断。

　　A.条件（1）充分，但条件（2）不充分。

　　B.条件（2）充分，但条件（1）不充分。

　　C.条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分。

　　D.条件（1）充分，条件（2）也充分。

　　E.条件（1）和（2）单独都不充分，条件（1）和条件（2）联合起来也不充分。

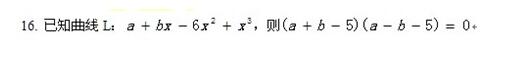
　　（1）曲线L过点（1,0）

　　（2）曲线L过点（-1,0）

　　解析：曲线L过点（1,0），带入Y=a+bx-6x?+x?则有Y=a+b-5=0，所以条件1充分

　　曲线L过点（-1,0），带入Y=a+bx-6x?+x?则有Y=a-b-7=0，则a-b=7，所以条件2不充分。所以答案选A

　　（1）已知BC的长

　　（2）已知AO的长

　　17题解析：绝对值不等式解集为空，则有-1≤X?+2X+a≤1的解集为空。

　　∵-1≤（X+1）?+a-1≤1

　　（X+1）?≥0

　　条件1，a＜0，得a-1＜-1，假设a=-2

　　（X+1）?-3≤1，所以x=1为一个解集，所以条件1不成立

　　条件2，a＞2，a-1＞1，（X+1）?+a-1＞1，所以条件2成立

　　所以答案选B

　　18题：解析：

　　条件一，甲乙丙年龄为等差数列，假设为2,4,6，与年龄相同不符合。

　　条件二，甲乙丙年龄成等比数列，假设为2,4,8，与年龄相同不符合。

　　若既为等差数列又为等比数列，则甲乙丙年龄相等。答案选C

　　19题：解析：X?+（1/Xm?）=（X+1/X）（X?+1/X?-1）=18

　　条件一，X+1/X =3 →（X+1/X）?=9 →X?+1/X?+2=9 →X?+1/X?=7

　　带入题干，得3*（7-1）=18

　　所以条件一符合。

　　条件二，X?+1/X?=7→（X+1/X）?-2* X*（1/X）=7→X+1/X=±3

　　带入题干，得±3*（7-1）=±18

　　所以条件二不符合。

　　所以答案选A

　　20题，解析：由圆性质可知，圆的直径与圆周相交的两点，与圆周上任意一点相连所得三角形都为直角三角形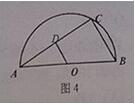

　　∴OD∥BC，O是AB的中点，所以A0/AB=OD/BC=1/2

　　条件一，已知BC的长，可知OD长，充分。

　　条件二，已知AO的长，不可知OD长，不充分。
　　所以答案选A。

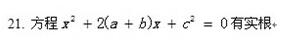
　　（1）a,b,c是三角形的三边长

　　（2）实数a, b，c成等差数列

　　解析：考察一元二次方程△=b?-4ac的判断。△＞0有两个相异的实根。△=0有两个相同的实根。△＜0无实根。

　　条件一，a,b,c是三角形的三边长，通过三角形性质可知a+b＞c，带入△判断

　　△=4（a+b）?-4c?＞0，有两个相异的实根，所以条件充分。

　　条件二，实数a, b，c成等差数列，则有a+c=2b。假设abc为1,3,5，带入△＜0，所以不充分

　　答案选A。

 

　　22题，解析：条件一，将点（0,0）和点（1,1）带入二次函数f（x），得c=0，a+b+c=1，即a+b=1，无法确定a，b值。不充分。

　　条件二，y=a+b，则直线y是平行于x轴的直线。f（x）是抛物线，两线相切，切点只能是抛物线顶点，即顶点坐标【-b/2a，（4ac-b?）/4a】，所以（4ac-b?）/4a=a+b，不充分。

　　考虑条件1+条件2，c=0，a+b=1，代入（4ac-b?）/4a=a+b，得a=-1，b=2，条件充分。所以答案选C

　　23题，解析：因为不知道三种颜色的球的数目，所以条件一和条件二都不充分。

　　考虑条件1+条件2，设红球a个，黑球b个，白球c个。

　　条件1，得c/（a+b+c）=2/5

　　条件2，可知随机取出两个球没有黑球的概率大于4/5，即C（2，a+c）/C（2，a+b+c）＞4/5

　　即（a+c）（a+c-1）/（a+b+c）（a+b+c-1）＞4/5

　　∵（a+c-1）/（a+b+c-1）＜1，∴（a+c）/（a+b+c）＞4/5

　　即【a/（a+b+c）】+【c/（a+b+c）】＞4/5

　　再由c/（a+b+c）=2/5

　　所以a/（a+b+c）＞2/5

　　所以b/（a+b+c）＜1/5

　　所以a最大，即红球最多。答案选C

　　24. 已知M={a，b，c，d，e}是一个整数集合，则能确定集合M

　　（1）a,b,c,d,e的平均数是10

　　（2）a,b,c,d,e的方差是2

　　解析：条件1和条件2单独都不充分。

　　考虑条件1+条件2：方差是各个数据与平均数之差的平方的和的平均数,

　　即S?=（1/n）【（x1-x）?+（x2-x）?+……+（xn-x）?】

　　→（1/5）【(a-10)?+ (b-10)?+ (c-10)?+ (d-10)?+ (e-10)?】=2

　　→(a-10)?+ (b-10)?+ (c-10)?+ (d-10)?+ (e-10)?=10

　　→a?+b?+c?+d?+e?-20（a+b+c+d+e）+5*10?=10

　　→a?+b?+c?+d?+e?=20*50-5*10?+10=510

　　由a+b+c+d+e=50，a?+b?+c?+d?+e?=510无法确定a,b,c,d,e的值，所以答案选E

　　解析：画数轴，√（x?+y?）表示点（x，y）到原点的距离。

　　条件1，若4x-3y≥5，d=√（x?+y?）≥5/√（3?+4?）=1，所以x?+y?≥1，充分。

　　条件2，简化不等式无法得出x?+y?≥1，不充分。

　　所以答案选A